Sequences and PatternsArithmetic and Geometric Sequences
In 1682, the astronomer
Halley remembered that other astronomers had observed similar comets much earlier: one in 1530 and another in 1606. Notice that the gap between two consecutive observations is the same in both cases:
Image of Halley’s Comet,
taken in 1986 on Easter Island
Halley concluded that all three observations were in fact of the same comet – which is now called Halley’s comet. It is orbiting around the sun and passes Earth approximately every 76 years. He also predicted when the comet would be visible next:
1530, 1606 +76, 1682 +76, 1758 +76,
Actually, the time interval is not always exactly 76 years: it can vary by one or two years, as the comet’s orbit is interrupted by other planets. Today we know that Halley’s comet was observed by ancient astronomers as early as 240 BC!
Depictions of Halley’s comet throughout time: a Babylonian tablet (164 BC), a medival tapestry (1070s), a science magazine (1910) and a Soviet stamp (1986).
A different group of scientists is investigating the behaviour of a bouncing tennis ball. They dropped the ball from a height of 10 meters and measured its position over time. With every bounce, the ball loses some of its original height:
The scientists noticed that the ball loses 20% of its height after every bounce. In other words, the maximum height of every bounce is 80% of the previous one. This allowed them to predict the height of every following bounce:
10, 8 ×0.8,
Definitions
If you compare both these problems, you might notice that there are many similarities: the sequence of Halley’s comet has the same
Sequences with these properties have a special name:
An
The same number is added or subtracted to every term, to produce the next one.
A
Every term is multiplied or divided by the same number, to produce the next.
Here are a few different sequences. Can you determine which ones are arithmetic, geometric or neither, and what the values of d and r are?
2, 4, 8, 16, 32, 64, …
is
2, 5, 8, 11, 14, 17, …
is
17, 13, 9, 5, 1, –3, …
is
2, 4, 7, 11, 16, 22, …
is
40, 20, 10, 5, 2.5, 1.25, …
is
To define an arithmetic or geometric sequence, we have to know not just the common difference or ratio, but also the initial value (called
Arithmetic Sequence
${arithmetic(a,d,0)}, ${arithmetic(a,d,1)}, ${arithmetic(a,d,2)}, ${arithmetic(a,d,3)}, ${arithmetic(a,d,4)}, ${arithmetic(a,d,5)}, …
Geometric Sequence
${geometric(b,r,0)}, ${geometric(b,r,1)}, ${geometric(b,r,2)}, ${geometric(b,r,3)}, ${geometric(b,r,4)}, ${geometric(b,r,5)}, …
Notice how all arithmetic sequences look very similar: if the difference is positive, they steadily
Geometric sequences, on the other hand, can behave completely differently based on the values of
If , the terms will
If , the terms will always
If , the terms will alternate between positive and negative, while their
You’ll learn more about convergence and divergence in the last section of this course.
Recursive and Explicit Formulas
In the previous section, you learned that a
One problem with recursive formulas is that to find the 100th term, for example, we first have to calculate the previous 99 terms – and that might take a long time. Instead, we can try to find an
For arithmetic sequences, we have to add d at every step:
At the nth term, we are adding
For geometric sequences, we have to multiply r at every step:
At the nth term, we are multiplying
Here is a summary of all the definitions and formulas you’ve seen so far:
An arithmetic sequence has first term
Recursive formula:
Explicit formula:
A geometric sequence has first term
Recursive formula:
Explicit formula:
Now let’s have a look at some examples where we can use all this!
Pay it Forward
Here is a short clip from the movie Pay it Forward, where 12-year-old Trevor explains his idea for making the world a better place:
The essence of Trevor’s idea is that, if everyone “pays it forward”, a single person can have a huge impact on the world:
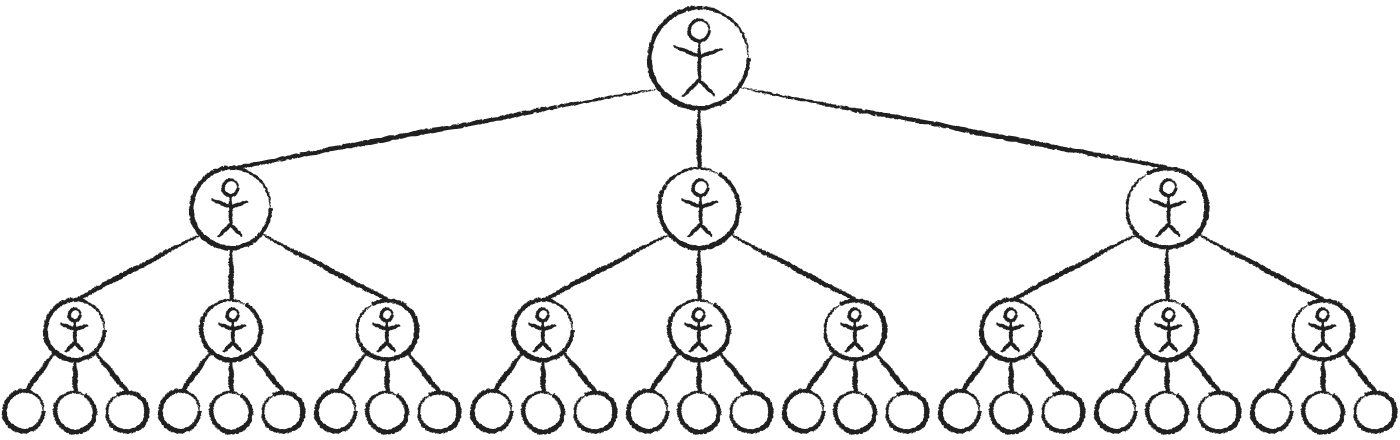
Notice how the number of people at every step forms a
1, 3 ×3, 9 ×3,
Using the
The number of people increases incredibly quickly. In the 10th step, you would reach 19,683 new ones, and after 22 steps you would have reached more people than are currently alive on Earth.
This sequence of numbers has a special name: the powers of 3. As you can see, every term is actually just a different
Who wants to be a Millionaire?
COMING SOON!
The Chessboard Problem
COMING SOON!